Закон равномерной плотности
В некоторых задачах практики встречаются непрерывные случайные величины, о которых заранее известно, что их возможные значения лежат в пределах некоторого определенного интервала; кроме того, известно, что в пределах этого интервала все значения случайной величины одинаково вероятны (точнее, обладают одной и той же плотностью вероятности). О таких случайных величинах говорят, что они распределяются по закону равномерной плотности.
Пример 1. Произведено взвешивание тела на точных весах, но в распоряжении взвешивающего имеются только разновески весом не менее \(1\) г; результат взвешивания показывает, что вес тела заключен между \(k\) и \((k+1)\) граммами. Вес тела принят равным \((k+\frac{1}{2})\) граммам. Допущенная
при этом ошибка \(X\), очевидно, есть случайная величина, распределенная с равномерной плотностью на участке \((-\frac{1}{2}, \frac{1}{2})\) г.
Пример 2. Вертикально поставленное симметричное колесо приводится во вращение и затем останавливается вследствие трения.
Рассматривается случайная величина \(\Theta\) — угол, который после остановки будет составлять с горизонтом фиксированный радиус колеса \(OA\). Очевидно, величина \(\Theta\) распределена с равномерной плотностью на участке \((0, 2\pi )\).
Пример 3. Поезда метрополитена идут с интервалом \(2\) мин.
Пассажир выходит на платформу в некоторый момент времени.
Время \(T\), в течение которого ему придется ждать поезда, представляет собой случайную величину
распределенную с равномерной плотностью на участке \((0, 2)\) минут.
Приведем несколько примеров подобных случайных величин.
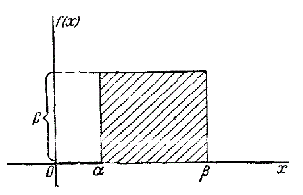
Рассмотрим случайную величину \(X\), подчиненную закону равномерной плотности на участке от \(\alpha\) до \(\beta\) (рис.1), и напишем для нее выражение плотности распределения \(f(x)\). Плотность \(f(x)\) постоянна и равна \(c\) на отрезке \((\alpha , \beta )\); вне этого отрезка она равна нулю:
Так как площадь, ограниченная кривой распределения, равна
Формула и выражает закон равномерной плотности на
участке \((\alpha , \beta )\).