Обозначения: \(\overline{AB},\,\overrightarrow{AB},\,\bar{a},\,\vec{a},\,a\).
Длина вектора, модуль (абсолютная величина): \(|\overline{AB}|, \, |\overrightarrow{AB}|, \, |\bar{a}|, \, |\vec{a}|, \, a\).
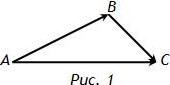
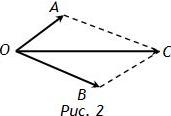
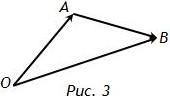
Сумма векторов
\(\overline{AB}+\overline{BC}=\overline{AC}\) (правило треугольника) (рис.1);
\(\overline{OA}+\overline{OB}=\overline{OC}\) (правило параллелограмма) (рис.2);
\(\overline{AA_1}+\overline{AA_2}+\ldots+\overline{A_{n-1}A_n}=\overline{AA_n}\) (правило многоугольника).
Разность векторов: \(\bar{a}-\bar{b}=\bar{a}+(-\bar{b})\).
Формула вычитания векторов: \(\overline{OB}-\overline{OA}=\overline{AB}\) (рис. 3).
Признак коллинеарности векторов: \(\bar{a}=\alpha \bar{b} \, (\bar{b}\neq 0)\).
Законы векторной алгебры
Для любых векторов \(\bar{a},\, \bar{b},\, \bar{c}\) и любых чисел \(\alpha,\: \beta\) справедливы равенства:
$$\bar{a}+\bar{b}=\bar{b}+\bar{a}$$
$$\bar{a}+(\bar{b}+\bar{c})=(\bar{a}+\bar{b})+\bar{c}$$
$$\bar{a}+\bar{0}=\bar{a}$$
$$(\alpha \beta )\bar{a}=\alpha (\beta \bar{a})$$
$$\alpha \bar{a}+\beta \bar{a}=(\alpha + \beta) \bar{a}$$
$$\alpha \bar{a}+\alpha \bar{b}= \alpha(\bar{a}+\bar{b})$$
$$0\cdot \bar{a}=\alpha \cdot \bar{0}=\bar{0}$$
Скалярное произведение
$$\bar{a} \cdot \bar{b}=|\bar{a}| \, |\bar{b}|\cos\varphi,$$
где \(\varphi\) - угол между векторами \(\bar{a}\) и \(\bar{b}\); если \(\bar{a}=0\) или \(\bar{a}=0\), то \(\bar{a} \cdot \bar{b}=0\).Скалярный квадрат вектора: \(\bar{a} \cdot \bar{a}=\overline{a^2}\).
Свойства скалярного произведения
$$\bar{a} \cdot \bar{b}=\bar{b} \cdot \bar{a}$$
$$(\alpha \bar{a}) \cdot \bar{b}=\alpha (\bar{a} \cdot \bar{b})$$
$$(\bar{a}+\bar{b}) \cdot \bar{c}=\bar{a} \cdot \bar{c}+\bar{b} \cdot \bar{c}$$
$$\bar{a} \cdot \bar{a}\geq 0$$
$$\bar{a} \cdot \bar{a}=0 \Leftrightarrow \bar{a}=\bar{0}$$
$$\bar{a} \cdot \bar{b}=0 \Leftrightarrow \bar{a} \perp \bar{b}$$
$$\overline{a^2}=|\bar{a}|^2$$Векторное произведение
Обозначается \([\overline{a\,b}], \: [\bar{a},\, \bar{b}], \:\bar{a}\times \bar{b}\).Свойства векторного произведения
$$[\bar{b}\, \bar{a}]=-[\bar{a}\, \bar{b}]$$
$$[(\alpha \bar{a})\, \bar{b}]=[\bar{a}(\alpha \bar{b})]=\alpha [\bar{a}\, \bar{b}]$$
$$[(\bar{a}+\bar{b})\bar{c}]=[\bar{a}\bar{c}]+[\bar{b}\bar{c}]$$
$$[\bar{c}(\bar{a}+\bar{b})]=[\bar{c}\bar{a}]+[\bar{c}\bar{b}]$$
$$[\bar{a}\bar{a}]=0$$
$$[\bar{a}\bar{b}]=\bar{0}\Leftrightarrow \bar{a}\parallel \bar{b}$$
2010-12-21 • Просмотров [ 3338 ]