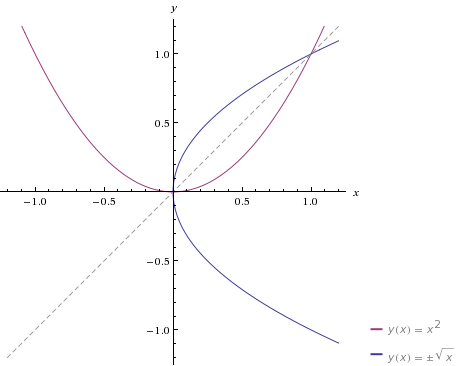
Для начала немного теории. Если есть функция \(y=f(x)\), то \(y\) зависит от аргумента \(x\). Но, получается что и наоборот, \(x\) зависит от \(y\), если из уравнения функции выразить \(x\) через \(y\). Если в этой зависимости переобозначить \(x\) и \(y\), то и получится обратная функция к данной. При этом графики обратных функций будут относительно биссектрисы первой и третьей четверти. На рисунке слева (кликнуть для увеличения), вы можете видеть графики двух взаимно обратных функций \(y=x^2\) и \(y=\pm\sqrt{x}\). Алгоритм нахождения обратной функции прост. Шаг первый: из данной функции выразить \(x\) через \(y\). Шаг второй: в полученном выражении поменять \(x\) на \(y\) и \(y\) на \(x\). Но, не всегда просто сделать эти преобразования. Поэтому, специально для наших посетителей предлагаем онлайн-решебник, который легко справится с задачей нахождения обратной функции и построит графики данной и обратной функции. Для этого Вам понадобится воспользоваться командой inverse и набрать в строке решателя Вашу функцию. Приведем несколько примеров команд для нахождения обратных функций.
inverse y=x^2inverse y = x^3+x^2+3x+5inverse y = sin(2x)+cos(2x)